В качестве примеров распределений непрерывной случайной величины приведем следующие часто используемые в задачах управления качеством распределения, которые понадобятся нам для дальнейшей работы.

 

Нормальное (гауссовское) распределение имеет вид

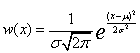                                                      .                                                   (1.18)

 

Здесь  - среднее,  - дисперсия распределения СВ.

 

На рисунке 1.1 приведен график дифференциального, а на рисунке 1.2 - интегрального гауссовского  распределений непрерывной СВ.

 

Рисунок 1.1.  Дифференциальное гауссовское распределение

 

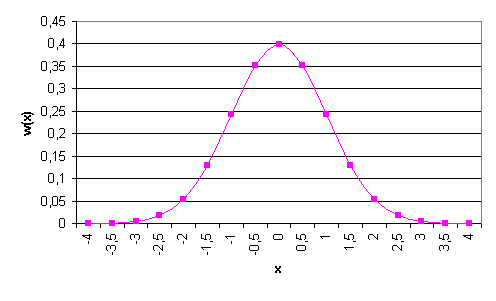
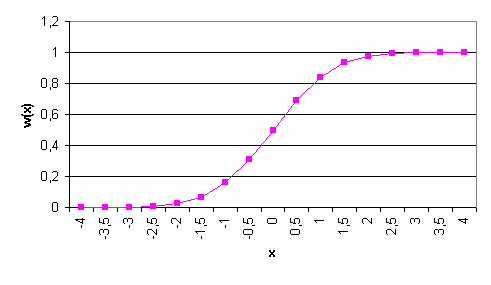
Рисунок 1.2. Интегральное гауссовское распределение

 

Равномерное (равновероятное) распределение на интервале [a,b] описывается соотношением

 

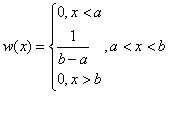                                                                                                   (1.19)

 

Среднее значение и дисперсия этого распределения равны соответственно

 

 ,  .

 

Распределение (хи –квадрат).  Если ,   - независимые нормально распределенные числа с нулевым  средним  и единичной дисперсией, то статистика (функция случайных величин)

 

                                                                                                                           (1.20)

 

подчиняется распределению   с  k степенями свободы.

 

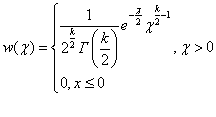                                                                                       (1.21)

 

Здесь 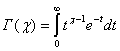   - гамма функция. Математическое ожидание и дисперсия данного распределения имеют вид соответственно     .

 

Распределение Стьюдента (t- распределение).  Пусть z – нормальная случайная величина с нулевым математическим ожиданием и единичной дисперсией. Пусть также v – независимая от z  СВ, имеющая   распределение  с k степенями свободы. Тогда СВ

 

                                                                                                                               (1.22)

 

имеет t- распределение с k степенями свободы

 

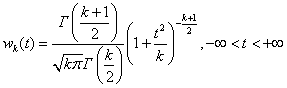                                                                     (1.23)

 

Среднее значение и дисперсия равны соответственно  .

 

Распределение Фишера-Снедекора.

Если u и v   независимые СВ, распределенные по закону   со    степенями свободы    и    соответственно, то  СВ

                                                                                                                             (1.24)

 

имеет  распределение  Фишера-Снедекора

 

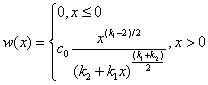                                                                                         (1.25)

 

Здесь 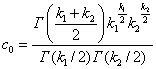.,  среднее значение и дисперсия равны соответственно

 

,    .

 

Приведем  примеры распределений дискретной СВ,  используемые в задачах управления качеством.

 

Гипергеометрическое распределение, часто применяемое в задачах выборочного контроля,   имеет вид

                                                                                             (1.26)

 

Здесь V -  объем контролируемой партии, N – число изделий в выборке,  k – число дефектных изделий в выборке, D – число дефектных изделий в партии,

 

 

 -  число сочетаний из D по k.

 

 

Среднее значение и дисперсия этого распределения равны соответственно

 

 

,         .

 

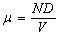В случае N<<V гипергеометрическое распределение хорошо аппроксимируется биномиальным  распределением,  вычисляемым по формуле

 

 

                                                                                               (1.27)

 

Здесь  -  вероятность дефекта, остальные обозначения соответствуют приведенным для гипергеометрического распределения.

 

Среднее значение и дисперсия для биномиального  распределения вычисляются соответственно по формулам

 

        ,         .

 

В случае если число испытаний N  возрастает, а вероятность q уменьшается так, что Nq=const,  биномиальное распределение стремится к  распределению Пуассона

 

                                                         .                                                      (1.28)

 

Здесь N – объем испытуемой выборки, k – число интересующих исследователя событий, происшедших в процессе испытаний,  - среднее  число событий в выборке (интенсивность потока событий). Среднее значение и дисперсия распределения Пуассона имеют вид 

 

20.1.1 Основные понятия теории вероятностей, используемые в задачах управления качеством