Как уже было отмечено выше,  функция распределения дает полное статистическое описание   СВ.   Распределение СВ  характеризуется   числовыми характеристиками, важнейшими из которых являются среднее значение и дисперсия. Характеристики распределений генеральных совокупностей можно оценить по выборочным данным. Оценки могут быть  несмещенными, эффективными и состоятельными. Несмещенной является оценка, среднее значение которой совпадает со средним значением соответствующей характеристики генеральной совокупности. Т.е.

 

.

 

Здесь  - оценка,  - истинное значение характеристики,  – оператор усреднения.

 

Эффективной называется оценка, которая из всех возможных вариантов оценок имеет минимальную дисперсию.

 

Состоятельной называется оценка, которая при увеличении объема выборки стремится к истинному значению по вероятности, т.е.

.

 

Рассмотрим наиболее важные с точки зрения  практики управления качеством  оценки математического ожидания  и дисперсии для случая гауссовских выборочных данных  (ГОСТ Р 50779.21-96).

 

Точечная оценка математического ожидания  определяется по формуле

                                                             .                                                          (2.10)

Поскольку значения  в этой формуле случайны и их число конечно, величина   также является случайной. При условии, что -  гауссовские  независимые числа,    является гауссовским случайным числом.  Покажем,  что среднее значение и дисперсия этого числа равны соответственно (среднее генеральной совокупности) и  , где - дисперсия отдельного отсчета.

Действительно,

                                                                   (2.11)

 

Для нахождения дисперсии  найдем  дисперсию отдельных слагаемых в последнем соотношении

 

                                                         (2.12)

 

 

Далее примем во внимание, что дисперсия суммы независимых слагаемых равна сумме дисперсий  этих слагаемых, т.е.

                                                                                                         (2.13)

 

 

Соотношения (2.11) и  (2.12) показывают, что оценка (2.10) является несмещенной и эффективной.

 

Точечная оценка дисперсии определяется по формуле

                                                                                                   (2.14)

 

Интервальная оценка математического ожидания для случая известной  дисперсии. Точечная оценка не позволяет определить, с какой вероятностью полученная величина оценки соответствуют истинному значению характеристики генеральной совокупности. Чтобы ответить на этот вопрос вводят понятие интервальной оценки.

Пусть - истинное среднее генеральной совокупности,   - точечная оценка , полученная по формуле (2.10). Введем доверительный интервал

 

                                                                                                                       (2.15)

 

где  - некоторое произвольное число, назначенное исследователем. Введем также доверительную вероятность  как вероятность того, что истинное значение среднего  попадет в записанный выше доверительный интервал, т.е.

                                                                                                 (2.16)

 

Чтобы вычислить  перейдем от абсолютных величин  и  к ошибкам в определении среднего  для чего вычтем  из всех частей неравенства (2.16). В результате получим

                                                                                                   (2.17)

 

Подставим в последнее соотношение  и с учетом того, что величина выборочного среднего  распределена по нормальному закону  ,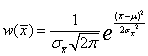

 

 

                           .                        (2.18)

 

Отсюда

                                                                           (2.19)

 

Здесь 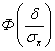 - интеграл вероятности, который имеет вид

                                                                                                           (2.20)

 

Обозначим   вероятность того, что истинное значение  выйдет за пределы доверительного интервала. Эта  вероятность называется уровнем значимости. Поскольку выход за пределы доверительного интервала возможен как справа, так и слева от его границ с одинаковой вероятностью, равной , из (2.19) следует соотношение

                                                                                                                   (2.21)

 

Обозначим  - квантиль уровня  стандартного гауссовского распределения (распределе

 

ние, для которого среднее значение равно нулю, дисперсия – единице). По определению квантиль удовлетворяет уравнению

                                                                                         (2.22)

 

Из (2.21) и (2.22) следует

                                                                                                                             (2.23)

Отсюда

                                                                                                                           (2.24)

 

Подставив (2.24)  в  (2.16), получим выражение для доверительного интервала

                                                                                                   (2.25)

Или с учетом (2.13)

                                                                                   (2.26)

 

Здесь  -  среднеквадратическое значение одиночного измерения.

Последнее соотношение в соответствии с ГОСТ Р 50779.21 – 96 называется интервальной оценкой генеральной средней, полученной по гауссовской выборке объема n для случая известной дисперсии.

 

Физический смысл этой оценки поясним следующим примером. Зададим уровень значимости . Отсюда следует = 3. В результате образуется доверительный интервал шириной ,

 

куда величина неизвестного генерального среднего  входит с вероятностью 1-0.0027=0.997.

 

Найдем интервальную оценку генеральной средней по выборочным данным для случая  неизвестной дисперсии. Как и в случае известной дисперсии выборочное среднее значение  (точечная оценка среднего) определяется по формуле (2.10). Аналогично записывается и доверительный интервал (2.15).  Однако далее при нахождения величины доверительного интервала , обеспечивающего заданную доверительную вероятность,  мы уже не можем воспользоваться гауссовской моделью относительной ошибки измерения  поскольку неизвестен параметр .  Вместо неизвестного значения    мы вынуждены использовать его точечную оценку   по формуле (2.14). В результате нормированная ошибка измерения   (после сокращения одинакового для числителя и знаменателя множителя  в числителе – гауссовская СВ с нулевым средним и единичной дисперсией, в знаменателе – величина, имеющая распределение ) будет иметь распределение Стьюдента с (n-1) степенями свободы (см. раздел 20.1.1.3) и для вычисления доверительной вероятности вместо интегрирования стандартного гауссовского распределения по формуле (2.19) необходимо интегрировать распределение Стьюдента. В результате формула (2.24) приобретает вид

 

                                                                                                                     (2.27)

 

Отсюда следует выражение для интервальной оценки генерального среднего при неизвестной  дисперсии  по ГОСТ Р 50779.21 – 96

 

                                                                   (2.28)

 

В соответствии с ГОСТ Р 50779.21 –96  интервальная оценка  дисперсии  при известном среднем определяется  по формуле

 

                                                         (2.29)

 

20.1.2 Оценки центра настройки и рассеяния  параметров технологических объектов